 La hidrodinámica estudia la dinámica de fluídos no compresibles. Por extensión, dinámica de fluidos.
La hidrodinámica estudia la dinámica de fluídos no compresibles. Por extensión, dinámica de fluidos.
Ésta es la dinámica del agua: ya que el prefijo griego “hidro-” significa “agua”. Aun así también incluye el estudio de la de otros fluidos. Para ello se considera entre otras cosas la velocidad, presión, flujo y gasto del fluido.
Las aplicaciones de la hidrodinámica se
encuentran en la ingeniería (diseño de canales, construcción de puertos,
presas, en la fabricación de barcos, turbinas,etc.).
Las ecuaciones que describen la dinámica de estos fluidos son las
ecuaciones de Navier-Stokes. Son la expresión matemática de la
conservación de masa y de cantidad de movimiento.
En el caso de fluidos no viscosos, también llamados fluidos
coloidales, se reducen a las ecuaciones de Euler. Daniel Bernoulli
fue uno de los primeros matemáticos que realizó estudios de
hidrodinámica, siendo precisamente él quien dio nombre a esta rama de la
física con su obra de 1738, Hydrodynamica.
Teorema de Torricelli
 El caudal o gasto es una de las magnitudes principales en el estudio de la hidrodinámica. Se define como el volumen de líquido
El caudal o gasto es una de las magnitudes principales en el estudio de la hidrodinámica. Se define como el volumen de líquido  que fluye por unidad de tiempo
que fluye por unidad de tiempo  . Sus unidades en el Sistema Internacional son los m3/s y su expresión matemática:
. Sus unidades en el Sistema Internacional son los m3/s y su expresión matemática:
El comportamiento cualitativo que normalmente evocamos con el término "efecto de Bernoulli", es el descenso de la presión del líquido en las regiones donde la velocidad del flujo es mayor. Este descenso de presión por un estrechamiento de una vía de flujo puede parecer contradictorio, pero no tanto cuando se considera la presión como una densidad de energía.
En el flujo de alta velocidad a través de un estrechamiento, se debe incrementar la energía cinética, a expensas de la energía de presión.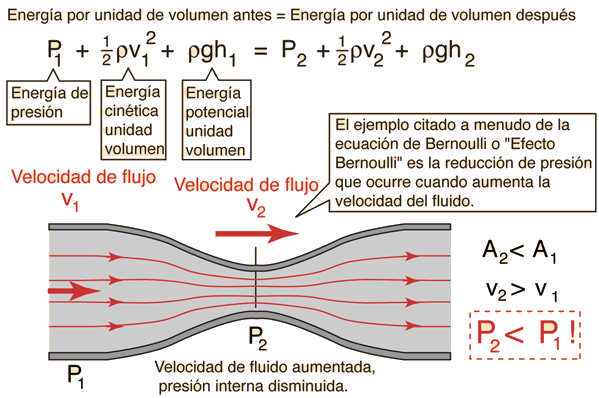
El principio de Bernoulli es una consecuencia de la conservación de la energía en los líquidos en movimiento. Establece que en un líquido incompresible y no viscoso, la suma de la presión hidrostática, la energía cinética por unidad de volumen y la energía potencial gravitatoria por unidad de volumen, es constante a lo largo de todo el circuito. Es decir, que dicha magnitud toma el mismo valor en cualquier par de puntos del circuito.
donde es la presión hidrostática,
es la presión hidrostática,  la densidad,
la densidad,  la aceleración de la gravedad,
la aceleración de la gravedad,  la altura del punto y
la altura del punto y  la velocidad del fluido en ese punto. Los subíndices 1 y 2 se refieren a los dos puntos del circuito.
la velocidad del fluido en ese punto. Los subíndices 1 y 2 se refieren a los dos puntos del circuito.
El cálculo en el "mundo real", de la presión en un estrechamiento de un
tubo, es dificil de hacer debido a las pérdidas por viscosidad,
turbulencia, y presunciones que se deben hacer sobre el perfil de la
velocidad (que afectan a la energía cinética calculada).
Características y leyes generales
La hidrodinámica o fluidos en movimientos presenta varias
características que pueden ser descritas por ecuaciones matemáticas muy
sencillas. Entre ellas:
Teorema de Torricelli
Establece que:
"La velocidad de un líquido que fluyendo por un orificio a través de una pared delgada es igual a la velocidad que tendría un cuerpo en caída libre de una altura “h”
El teorema de Torricelli o principio de Torricelli es una aplicación del principio de Bernoulli y estudia el flujo de un líquido contenido en un recipiente, a través de un pequeño orificio, bajo la acción de la gravedad.
A partir del teorema de
Torricelli se puede calcular el caudal de salida de un líquido por un
orificio.
donde:
- es la velocidad teórica del líquido a la salida del orificio
- es la velocidad de aproximación o inicial.
- es la distancia desde la superficie del líquido al centro del orificio.
- es la aceleración de la gravedad
Para velocidades de aproximación bajas, la mayoría de los casos, la expresión anterior se transforma en:
donde:
 es la velocidad real media del líquido a la salida del orificio
es la velocidad real media del líquido a la salida del orificio es el coeficiente de velocidad. Para cálculos preliminares en aberturas
de pared delgada puede admitirse 0,95 en el caso más desfavorable.
es el coeficiente de velocidad. Para cálculos preliminares en aberturas
de pared delgada puede admitirse 0,95 en el caso más desfavorable.
tomando  =1
=1
 =1
=1
- Experimentalmente se ha comprobado que la velocidad media de un
chorro de un orificio de pared delgada, es un poco menor que la ideal,
debido a la viscosidad del fluido y otros factores tales como la tensión
superficial, de ahí el significado de este coeficiente de velocidad.
Caudal o Gasto
 El caudal o gasto es una de las magnitudes principales en el estudio de la hidrodinámica. Se define como el volumen de líquido
El caudal o gasto es una de las magnitudes principales en el estudio de la hidrodinámica. Se define como el volumen de líquido  que fluye por unidad de tiempo
que fluye por unidad de tiempo  . Sus unidades en el Sistema Internacional son los m3/s y su expresión matemática:
. Sus unidades en el Sistema Internacional son los m3/s y su expresión matemática:
Esta fórmula nos permite saber la cantidad de líquido que pasa por un
conducto en cierto intervalo de tiempo o determinar el tiempo que
tardará en pasar cierta cantidad de líquido.
Actividad
Copia del siguiente video los ejercicios que se presentan para calcular el Caudal o Gasto de flujo de un liquido.
Actividad
Principio de Bernoulli (Teorema General de la Hidrodinámica)
La ecuación de Bernoulli, se puede considerar como una apropiada declaración del principio de la conservación de la energía, para el flujo de fluidos.El comportamiento cualitativo que normalmente evocamos con el término "efecto de Bernoulli", es el descenso de la presión del líquido en las regiones donde la velocidad del flujo es mayor. Este descenso de presión por un estrechamiento de una vía de flujo puede parecer contradictorio, pero no tanto cuando se considera la presión como una densidad de energía.
En el flujo de alta velocidad a través de un estrechamiento, se debe incrementar la energía cinética, a expensas de la energía de presión.

El principio de Bernoulli es una consecuencia de la conservación de la energía en los líquidos en movimiento. Establece que en un líquido incompresible y no viscoso, la suma de la presión hidrostática, la energía cinética por unidad de volumen y la energía potencial gravitatoria por unidad de volumen, es constante a lo largo de todo el circuito. Es decir, que dicha magnitud toma el mismo valor en cualquier par de puntos del circuito.
donde
 es la presión hidrostática,
es la presión hidrostática,  la densidad,
la densidad,  la aceleración de la gravedad,
la aceleración de la gravedad,  la altura del punto y
la altura del punto y  la velocidad del fluido en ese punto. Los subíndices 1 y 2 se refieren a los dos puntos del circuito.
la velocidad del fluido en ese punto. Los subíndices 1 y 2 se refieren a los dos puntos del circuito.
Cálculo de Bernoulli
El modelo de
cálculo de aquí, asume un flujo laminar (sin turbulencia), tambien asume que la distancia del diámetro mayor al menor es suficientemente pequeña para despreciar las pérdidas por viscosidad y asume que el perfil de la velocidad
sigue el del flujo laminar teórico. En concreto, esta asumiendo que la
velocidad de la corriente efectiva es la mitad de la velocidad máxima, y
que la densidad media de energía cinética está dada por un tercio de la
densidad de energía cinética máxima.
Practica la aplicación de Principio de Bernoulli accesando al siguiente sitio:
 es el área de la sección del conducto por donde circula el fluido y
es el área de la sección del conducto por donde circula el fluido y  su velocidad media.
su velocidad media.

 (el caudal que entra es igual al que sale)
(el caudal que entra es igual al que sale)
Practica la aplicación de Principio de Bernoulli accesando al siguiente sitio:
Ecuación de continuidad
La otra ecuación que cumplen los fluidos no compresibles es laque establece que el caudal es constante a lo largo de todo el circuito hidráulico:donde
 es el área de la sección del conducto por donde circula el fluido y
es el área de la sección del conducto por donde circula el fluido y  su velocidad media.
su velocidad media.
Cuando un fluido fluye por un conducto de diámetro variable, su
velocidad cambia debido a que la sección transversal varía de una
sección del conducto a otra.
En todo fluido incompresible, con flujo estacionario (en régimen
laminar), la velocidad de un punto cualquiera de un conducto es
inversamente proporcional a la superficie, en ese punto, de la sección transversal de la misma.
La conservación de la masa de fluido a través de dos secciones (sean éstas A1 y A2) de un conducto (tubería) o tubo de corriente establece que: la masa que entra es igual a la masa que sale.
Definición de tubo de corriente: superficie formada por las líneas de corriente.
Corolario 2: solo hay flujo de corriente si V es diferente de 0.
La ecuación de continuidad se puede expresar como:
Cuando  , que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
, que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
 , que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
, que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
o de otra forma:
 (el caudal que entra es igual al que sale)
(el caudal que entra es igual al que sale)
Donde:
- Q = caudal (metro cúbico por segundo;
 )
) - V = velocidad

- A = area transversal del tubo de corriente o conducto

Que se cumple cuando entre dos secciones de la conducción no se
acumula masa, es decir, siempre que el fluido sea incompresible y por lo
tanto su densidad sea constante. Esta condición la satisfacen todos los líquidos y, particularmente, el agua.
Ejemplo:
Un caudal de agua circula por una tubería de 1 cm de sección interior a una velocidad de 0,5 m/s. Si deseamos que la velocidad de circulación aumente hasta los 1,5 m/s, ¿qué sección ha de tener tubería que conectemos a la anterior?
Aplicando la ecuación de continuidad:
Sustituyendo por la expresión de la superficie del círculo:
Simplificando y despejando:
Sustituyendo:

Un caudal de agua circula por una tubería de 1 cm de sección interior a una velocidad de 0,5 m/s. Si deseamos que la velocidad de circulación aumente hasta los 1,5 m/s, ¿qué sección ha de tener tubería que conectemos a la anterior?
Aplicando la ecuación de continuidad:

Sustituyendo por la expresión de la superficie del círculo:

Simplificando y despejando:

Sustituyendo:


ACTIVIDAD
Resuelve el PROBLEMARIO de la unidad consultando el contenido del blog, y el siguiente sitio:
http://www.fisicanet.com.ar/fisica/estatica_fluidos/ap01_estatica_fluidos.php 


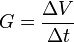



No hay comentarios:
Publicar un comentario